For this question, we can use the identity (abc) 2 = a 2 b 2 c 2 2ab abc 2ca (abc) 2 = 250 2(ab bc ca) (abc) 2 = 250 2(3) (abc) 2 = 250 6 (abc) 2 = 256 abc = square root of 256 abc = 16 There you go Hope it helps! Transcript Misc 13 Using properties of determinants, prove that 3a ab ac ba 3b bc ca cb 3c = 3 ( a b c) (ab bc ac) Taking LH S 3a ab ac ba 3b bc ca cb 3c Applying C1 C1 C2 C3 = 3a ab ac ab ac ba 3b bc 3b bc ca cb 3c cb 3c = ab ac 3b bc cb 3c Taking (a b c) common from C1 = ( ) 1 abIn algebra, a quadratic equation (from the Latin quadratus for "square") is any equation that can be rearranged in standard form as = where x represents an unknown, and a, b, and c represent known numbers, where a ≠ 0If a = 0, then the equation is linear, not quadratic, as there is no term The numbers a, b, and c are the coefficients of the equation and may be distinguished by calling
If You Are Given A B C Ab Ac 0 Then How Will You Show That A B C Quora
(ab+bc+ca)^3 formula
(ab+bc+ca)^3 formula-$$(a b c)^3 = (a^3 b^3 c^3) 3a(ab ac bc) 3b(ab bc ac) 3c(ac bc ab) 3abc$$ $$(a b c)^3 = (a^3 b^3 c^3) 3(a b c)(ab ac bc) 3abc$$ $$(a b c)^3 = (a^3 b^3 c^3) 3(a b c)(ab ac bc) abc$$ It doesn't look like I made careless mistakes, so I'm wondering if the statement asked is correct at allThe area of whole square is ( a b c) 2 geometrically The whole square is split as three squares and six rectangles So, the area of whole square is equal to the sum of the areas of three squares and six rectangles ( a b c) 2 = a 2 a b c a a b b 2 b c c a b c c 2 Now, simplify the expansion of the a b c whole




What Are Various Forms To Write A B C A Whole Cube Quora
Math formula is very important for solving math problems Here you can find All Mathematical formulas which you need in Competitive exams 21 Learn these basic mathematical formula a 3 b 3 c 3 – 3abc = (a b c)(a 2 b 2 c 2 – ab – bc – ca) If a b c = 0, then the above identity reduces to a 3 b 3 c 3 = 3abc;Without loss of generality, we may suppose that AD is the minimum side (1) When AB=AD, we have BC=CD In this case, letting O be the intersection point of AC and the bisector of \angle B,(4) If in the figure below AB = 15 cm, BC= cm and CA = 7 cm, find the area of the rectangle BDCE (5) The area of a trapezium is 98 cm 2 and the height is
Hence we have the other factor = (a2 b2 c2) k (ab bc ca) ;A3 −b3 =(a−b)33ab(a−b) 6 a2 −b2 =(ab)(a−b) 7 a3 −b3 =(a−b)(a2 ab b2) 8 a3 b3 =(ab)(a2 −ab b2) 9 a n−bn=(a−b)(an−1 a −2b an−3b2 Example 11 If a b c = 9 and ab bc ca = 40, find a 2 b 2 c 2 Solution We know that Example 12 If a 2 b 2 c 2 = 250 and ab bc ca = 3, find a b c Solution We know that Example 13 Write each of the following in expanded form (i) (2x 3y) 3 (ii) (3x – 2y) 3 Solution Example 14 If x y = 12 and xy = 27, find the value of x 3 y 3
= sin sin sinAB C 000 31 3 1 sin15 sin75 sin90 1 22 22 − == =− () 31 3 122() 7 Prove tht 2 cos c cos cos{bcA a Bab Cab =} 22 2c LHS 2 cos 2 cos 2 cosbc A ca B ab c From cosine rule 2 22 2 2 2 cos cos 22 bc a a c b AB bc ac − − ==The actual formula is (abc)² = a² b² c² 2 (ab bc ca) You can get this simple formula by multiplying (ab c) with (abc) (ab c)² = (ab c)* (ab c)RD Sharma Class 9 Solutions Chapter 12 Heron's Formula RD Sharma Class 9 Solution Chapter 12 Heron's Formula Ex 121 Question 1 In the figure, the sides BA and CA have been produced such that BA = AD and CA = AE




The Expression A B 3 B C 3 C A 3 Can Be Factorized A




Algebraic Identities Of Polynomials A Plus Topper
Section Formula With Examples Type I On finding the section point when the section ratio is given Example 1 Find the coordinates of the point which divides the line segment joining the points (6, 3) and (– 4, 5) in the ratio 3 2 internally Sol Let P (x, y) be the required point Given #v= 2(ab bc ca)#, how do you solve for a?b2 =(ab)2−2ab 2 (a−b)2 = a 2−2ab b;




What Will Be A B C If A B C 1 And Ab Ca 1 3 Quora



What Is The Expansion Of A B C 3 Quora
1 (a b)2 = a2 2ab b2;If P, Q and R are the midpoints of the sides, BC, CA and AB of a triangle and AD is the perpendicular from A on BC, then prove that P, Q, R and D are concyclic asked in Class IX Maths by aman28 (872 points) circles Categories AllHence the other factor, (a2 b2 c2 ab bc ca)



If A B C 9 And B2 C2 35 Then Find A3 C3 3abc Polynomials Maths Class 9




Xz X X Y Y Or Yx Y B2 C2 43 And Ab Ca 3 Gauthmath
Justify whether it is true to say that 1,3/2,2,5/2forms an AP as a2 a1 = a3 a2 asked in Class X Maths by akansha Expert ( 22k points) arithmetic progressionsIf a^2b^2c^2abbcca=0 then prove that a=b=c Get the answer to this question along with unlimited Maths questions and prepare better for JEE exam3 views asked 1 hour ago in 3D Coordinate Geometry by Harshal01 ( 110 points) The coordinates of the midpoints of sides AB, BC and CA of ΔABC are D(1, 2, 3), E(3, 0, 1) and F(1, 1,




Curved Line In Formulas Tex Latex Stack Exchange




A B 2 B C C A B C 2 A B C A C A 2 A B B C Brainly In
Exercise 91 Question 1 Identify the terms, their coefficients for each of the following expressions Answer Term x x Coefficient = 1 = 1 and Term x2 x 2 Coefficient = 1 Answer 1 2 1 2 is the coefficient for x and y and for xy it is 1 Answer 03 is the coefficient for a, for b there are two coefficients 06 and 05 a 3 − b 3 = (a − b) (a 2 b 2 ab) a 3 b 3 = (a b) (a 2 b 2 − ab) (a b c) 3 = a 3 b 3 c 3 3 (a b) (b c) (c a) a 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 − ab − bc − ac) If (a b c) = 0, a 3 b 3 c 3 = 3abcA^2 b^2 = (a – b)^2 2ab (a – b)^2 = a^2 – 2ab b^2 (a b c)^2 = a^2 b^2 c^2 2ab 2ac 2bc (a – b – c)^2 = a^2 b^2 c^2 – 2ab – 2ac 2bc (a b)^3 = a^3 3a^2b 3ab^2 b3 (a b)^3 = a^3 b^3 3ab (a b) (a – b)^3 = a^3 – 3a^2b 3ab^2 –




What Are Various Forms To Write A B C A Whole Cube Quora




If A B C 2 Ab Ca 1 And Abc 1 And Abc 2 Find The Value Of
b2 =(a−b)22ab 3 (a b c)2 = a2 b2 c2 2(ab bc ca) 4 (a b) 3= a3 b3 3ab(a b);Click here👆to get an answer to your question ️ If a^2 b^2 c^2 = 250 and ab bc ca = 3 , then find a b c Get the list of basic algebra formulas in Maths at BYJU'S Stay tuned with BYJU'S to get all the important formulas in various chapters like trigonometry, probability and so on




Q3 Add The Following I Ab Ca Ca Ab Ii A B Ab B C Lido




The Value Of The Determinant Ca Ab Where A B C Are The Pth Qth And Rth Terms Of A Hp Is P Q R 1 1 1 Mathematics Topperlearning Com Cg6ee
AP CALCULUS AB & BC FORMULA LIST Definition of e 1 lim 1 n n e of n §¨¸ ©¹ _____ Absolute value 0 0 x if x x x if x t ® ¯ _____ Definition of the derivative 0 ( ) lim h f x h f x fx o h c lim xa f x f a fa o xa c (Alternative form) _____ Definition of continuity f isExample Solve 8a 3 27b 3 125c 3 30abc Solution This proceeds as Given polynomial (8a 3 27b 3 125c 3 30abc) can be written as (2a) 3 (3b) 3 (5c) 3 (2a)(3b)(5c) And this represents identity a 3 b 3 c 3 3abc = (a b c)(a 2 b 2 c 2 ab bc ca) Where a = 2a, b = 3b and c = 5c Now apply values of a, b and c on the LHS of identity ie a 3 b 3 c 3 Multiply both sides with 2, we get 2 ( a2 b2 c2 – ab – bc – ca) = 0 ⇒ 2a2 2b2 2c2 – 2ab – 2bc – 2ca = 0 ⇒ (a2 – 2ab b2) (b2 – 2bc c2) (c2 – 2ca a2) = 0 ⇒ (a –b)2 (b – c)2 (c – a)2 = 0 Since the sum of square is zero then each term should be zero ⇒ (a –b)2 = 0, (b – c)2 = 0, (c – a)2 = 0




If A B C 2 Ab Ca 1 And Abc 1 And Abc 2 Find The Value Of
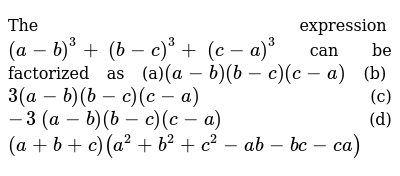



The Expression A B 3 B C 3 C A 3 Can Be Factorized A
#vinodmaths a³b³c³3abc=(abc)(a²b²c²abbcca) formula based questions This video is useful for all competitive exams specially ssc and delhi SI HereAP CALCULUS AB and BC Final Notes Trigonometric Formulas 1 sin θcos 2 θ=1 2 1tan θ=sec 2 θ 3 1cot θ=csc 2 θ 4 θ sin(−θ) =−sinθ 5If a b c = 9 and ab bc ca = 26, find the value of a 3 b 3 c 3 − 3abc Advertisement Remove all ads Solution Show Solution In the given problem, we have to find value of `a^3 b^3 c^3 3abc` Given `abc = 9, ab bc ca = 26` We shall use the identity



What Is The Formula For A B C Quora




If If A B C Are All Non Zero And A B C 0 Prove That B2 Ca C2 Ab 3 Mathematics Topperlearning Com 2jnu5w66
(abbcca)² = (ab) ²(bc)²(ca)²2(ab)(bc)2(bc)(ca)2(ca)(ab) hence, (ab)²(bc)²(ca)²2ab²c2abc²2a²bc (ab)²(bc)²(ca)²2abc(bca)Example Solve 8a 3 27b 3 125c 3 – 90abc Solution This proceeds as Given polynomial (8a 3 27b 3 125c 3 – 90abc) can be written as (2a) 3 (3b) 3 (5c) 3 – 3(2a)(3b)(5c) And this represents identity a 3 b 3 c 3 3abc = (a b c)(a 2 b 2 c 2 ab bc ca) Where a = 2a, b = 3b and c = 5c Now apply values of a, b and c on the LHS of identity ie a 3 b 3 c 3(abc)^2 >hoac=3(abbcca) giup minh moi minh dang can gap Theo dõi Vi phạm YOMEDIA Trả lời (1) (abc) 2 \(\ge\) 3(abbcca) (*) =>a 2 b 2 c 2 2ab2bc2ca \(\ge\) 3ab3bc3ca =>a 2 b 2 c 2 \(\ge\) abbcca nhân 2 vào cho 2 vế ta được 2a 2 2b 2



1




If A 2 B 2 C 2 1 Then Ab Ca Lies In The Interval Youtube
Solution for ABBC=AC equation Simplifying AB BC = AC Solving AB BC = AC Solving for variable 'A' Move all terms containing A to the left, all other terms to the right Add '1AC' to each side of the equation AB 1AC BC = AC 1AC Combine like terms AC 1AC = 0 AB 1AC BC = 0 Add '1BC' to each side of the equation a^3 b^3 c^3 a 3 b 3 c 3 = (a b c) (a 2 b 2 c 2 – ab – bc – ca) 3abc s Algebra, cube, sum, sum of cubes This entry was posted on at 554 pm and is filed under Algebra You can follow any responses to this entry through the RSS feed You can leave a response, or trackback from your own site=V384∠124 ca= 2°are applied to an inductionmachine The average value of the magnitudes will be (576 480 384)/3 = 480 V and the maximum deviation from average value is (576 480) = 96 V Therefore, the NEMA definition of % voltage unbalancewill be 100(96/480) = % The positive sequence voltage isV




A3b3c3 3abc Formula Proof រ បភ ពប ល ក Images




Xz X X Y Y Or Yx Y B2 C2 43 And Ab Ca 3 Gauthmath
A3 b3 =(ab)−3ab(a b) 5 (a−b)3 = a3 −b3 −3ab(a−b);Recall the formula ` (abc)^2 = a^2 b^2 c^2 2 (ab bc ca)` Given that `a^2 b^2 c^2 = 250 , ab bc ca = 3 ` Then we have ` (abc)^2 = a^2 b^2 c^2 2 (ab bcca)` ` (abc)^2 = 250 2 (3)` ` (abc)^2 = 256` ` (abc) =± 16`If abc=8 and abbcca= Find the value of a3b3c3−3abcHow to do it null null null null abc=8abbcca=a3b3c3=abca2b2c2−ab−bc−ca3abc⇒a3b3c3−
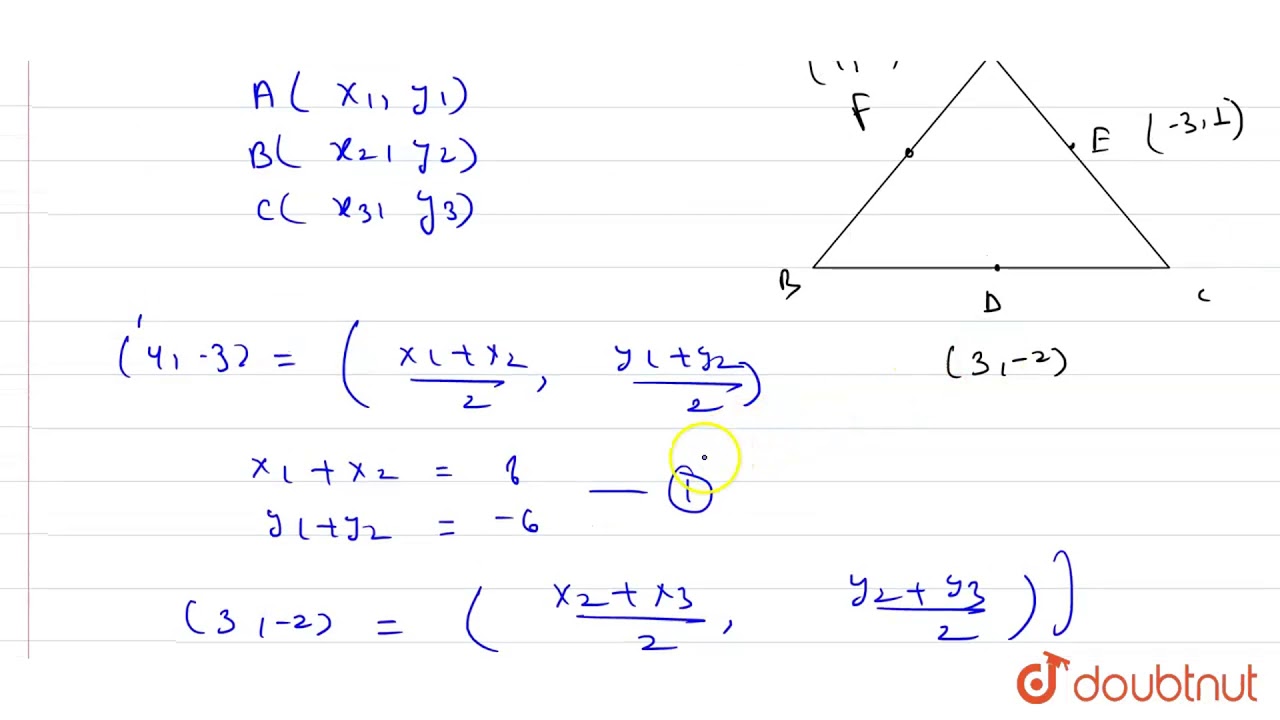



Let D 3 2 E 3 1 And F 4 3 Be The Midpoints Of The Sides Ca Youtube
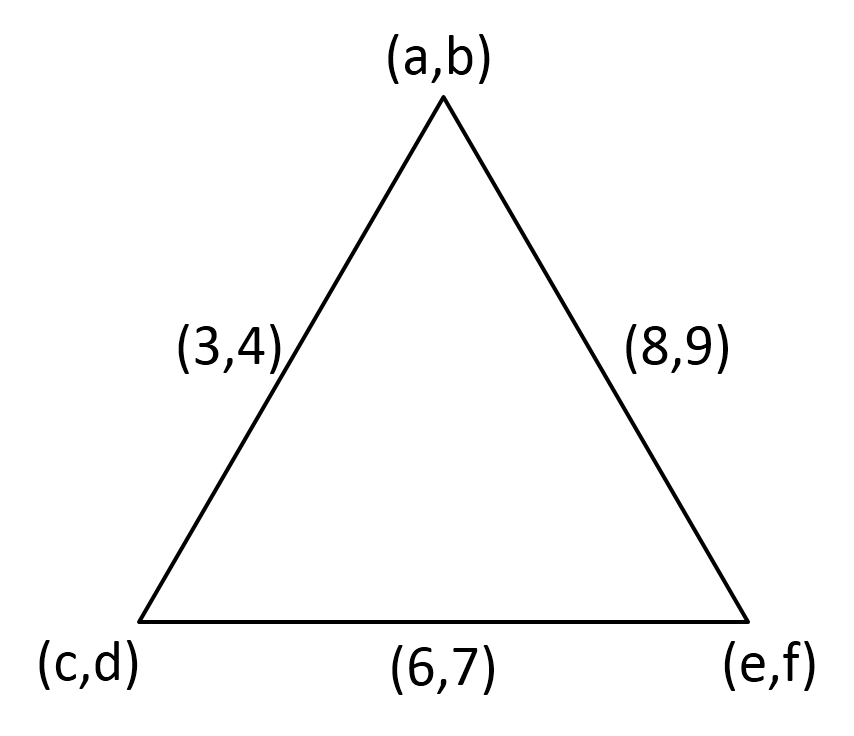



The Midpoints Of The Sides Ca And Ab Of A 8710 Abc Are D 3 4 E 8 9 And F 6 7 Respectively Find The Coordinates Of The Vertices Of The Triangle Mathematics Topperlearning Com Le8c5q
Algebra Linear Equations Formulas for Problem Solving 1 Answer P dilip_k What is the perimeter of the rectangle if the area of a rectangle is given by the formula How do you find the value of y that makes (3,y) a solution to the equation #3xy=4#?Simplify a b c = 25 and ab bc ca = 59 Find the value of a 2 b 2 c 2 Solution According to the question, a b c = 25 Squaring both the sides, we get (a b c) 2 = (25) 2 a 2 b 2 c 2 2ab 2bc 2ca = 625 a 2 b 2 c 2 2(ab bc ca) = 625 a 2 b 2 c 2 2 × 59 = 625 Given, ab bc ca = 59 a 2 b 2 c 2 118 = 625Click here👆to get an answer to your question ️ If a^2 b^2 c^2 ab bc ca = 0 , prove that a = b = c




What Will Be A B C If A B C 1 And Ab Ca 1 3 Quora




If A B C 2 Ab Ca 3 And Abc 4 Then Find The Value Of A B C Brainly In
Abc (1/a 1/b 1/c) = (3) (−2) bc ca ab = −6 Using the a 2 b 2 c 2 formula, a 2 b 2 c 2 = (a b c) 2 2 (ab bc ca) a 2 b 2 c 2 = (3) 2 2 (6) = 9 12 = 21 Answer a 2 b 2 c 2 = 21 Example 3 Find the value of a 2 b 2 c 2 if a b c = and ab bc ca = 100Where k is any integer (since net coefficients are integers) Now ((a2 b2 c2) k (ab bc ca) ) (abc) = a3b3c3−3abc The value of can be easily found out to be 1 (even by simply multiplying and comparing);Volume = (1/3)Π r²h L ² = r ² h² sphere Curved surface area = 4Π r² Volume = (4/3)Π r³ Hemisphere Curved surface area = 2Π r² Total Curved surface area=3Π r² Volume = (2/3)Π r³ Cuboid Curved surface area=4h(lb) Total surface area = 2(lbbhh l) Volume = l x b x h Cube Curved surface area=4a ² Total surface area = 6a² Volume = a ³




Find The Value Of A 3 B 3 C 3 3abc If 1 A B C 8 Ab Ca 19



How To Prove Math A 2 B 2 C 2 Ab Ca Math Is Non Negative For All Values Of Math A B Math And Math C Quora
The Formula is given below (a b c)³ = a³ b³ c³ 3 (a b) (b c) (a c) \(=> (abc)^3 = (a^3ab^2ac^2 2a^2b 2abc 2ca^2)\\ (a^2bb^3bc^2 2ab^2 2b^2c 2abc)\\ (ca^2 cb^2 c^3 2abc 2bc^2 2c^2a) \) Arrage value according power and similear \(=> (abc)^3 = a^3 b^3 c^3 \\ 6abc 3a^2b 3ab^2 \\ 3ac^2 3bc^2 3b^2c 3a^2c \)16 ejercicios resueltos productos notables nivel preuniversitarioTeoría https//wwwyoutubecom/watch?v=Qjes17MQXac




If A 2 B 2 C 2 Ab Ca 0 A B C In R Then Find The Value O



What Is The Expansion Of A B C 3 Quora




Q3 Add The Following I Ab Ca Ca Ab Ii A B Ab B C Lido




Ex 9 3 25 If A B C D Are In Gp Show B2 C2




Mathematics Formulas Classical Geometry Geometric Shapes




Factorise A B 3 B C 3 C A 3 Maths Polynomials Meritnation Com




What Are Various Forms To Write A B C A Whole Cube Quora




If A B C 0 Then Prove That B C 2 3bc C A 2 3ca A B 2 3ab 1 Mathematics Topperlearning Com Sq6lgh




Prove That The Following Determinant Is Equal To Ab Ca 3 B2 C2 Ac Ac C2 Brainly In




If A3 C3 3abc 1 2 A B C A B 2 B C 2 C A 2 Brainly In




Ex 9 1 3 I Add Ab Ca Ca Ab Chapter 9 Class 8




If X A X B X C Equiv X Sup3 10x Sup2 45x 15 Find A B C 1 A 1 B 1 C And A Sup2 B Sup2 C Sup2 7z7gic33 Mathematics Topperlearning Com




If A B C 6 A 2 B 2 C 2 14 A 3 B 3 C 3 36 Find Abc Youtube




How To Prove Math A 2 B 2 C 2 Ab Ca Math Is Non Negative For All Values Of Math A B Math And Math C Quora




What Are Various Forms To Write A B C A Whole Cube Quora




Misc 4 Show That Either A B C 0 Or A B C Miscellaneous




Prove That A B C 3 A 3 B 3 C 3 3 A B B C C A Youtube




If A B C Is Equals To 6 And A B Ca Is Equals To 11 Find A Cube Plus B Cube Plus C Cube Brainly In




What Are Various Forms To Write A B C A Whole Cube Quora




Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf



If You Are Given A B C Ab Ac 0 Then How Will You Show That A B C Quora




If B2 C2 280 And Ab Ca 9 2 Find The Value Of A B C 3 Mathematics Topperlearning Com 8438




Prove That A 2 B 2 C 2 Ab Ca Is Always Non Negative For All Valuesof A B And C Brainly In



How Do You Factor A B C Ab Ca Abc Socratic




Productos Notables Ejemplos Y Ejercicios Resueltos Pdf




What Is The Expansion Of A B C 3 Quora




If A B C 5 And Ab Ca 10 Then Prove That A3 C3 3abc 25 Mathematics Topperlearning Com T5wmjn




Math 9 Flip Book Pages 101 150 Pubhtml5




Important Question With Trick Powerpoint Slides




Misc 13 Using Determinants 3 A B C Ab Ac




Prove That A B C 3 A3 C3 3 A B B C C A Brainly In
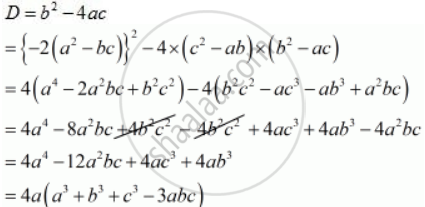



If The Roots Of The Equation C2 Ab X2 2 X B2 Ac 0 In X Are Equal Then Show That Either A 0 Or A3 C3 3abc Mathematics Shaalaa Com




Factorise A B B C C A Brainly In




A3 C3 3abc Formula Proof Advance Math Formula Proof In Easy Method Youtube




Prove A 3 B 3 C 3 3abc 1 2 A B C A B 2 B C 2 C A 2



Prove That A B C 3 A3 C3 3 A B B C C A Studyrankersonline




I Found K A B B C C A But What Is The Chegg Com




A B C 12 And B2 C2 50 Find Ab Ca Brainly In




Mitra Maths Prove That A3 C3 3abc A B C B2 C2 Ab Ca 1 2 A B C A B 2 B C 2 C A 2 Youtube




A Square Plus B Square Plus C Square Formula Examples A 2 B 2 C 2 Formula



1




Quadratic Equation Session1 Ppt Video Online Download



1




A B 3 B C 3 C A 3 A A B C A 2 B 2 C 2 Ab Ac B 3 A B B C C A C Youtube



What Is The Formula For A B C Quora



If B2 C2 Ab Ca 0 Prove That A B C Polynomials Maths Class 9




Maths Formulas For Cat 2 Euclidean Geometry Euclidean Plane Geometry




Prove A3 C3 3abc A B C B2 C2 Ab Ac Youtube




If A 2 B 2 C 2 250 And Ab Ca 3 Then Find A B C




Q17 A B 3 B C 3 C A 3 A A B C A 2 B 2 C 2 Ab Ca B A B B C C A




Algebraic Identities For Ssc Cgle Online Preparation Platform




Show That A B 3 B C 3 C A 3 3 A B B C C A Brainly In



The Mid Points Of The Sides Ab And Ca Of A Triangle Abc Are D 2 1 E 1 0 And F 1 3 Respectively Find The Coordinates Of The Vertices



If A B C 7 And Ab Ca Find The Value Of A 2 B 2 C 2 Polynomials Maths Class 9




Prove That A B 3 B C 3 C A 3 3 A B B C C A 2 A 3b 3c 3 3abc Brainly In




A B B C C A In G P Prove That A B C 2 3 Ab Ca Brainly In




Find A3 C3 3abc When A B C 15 Ab Ca 74 Brainly In




If A B C 6 And Ab Ca 11 Find The Value Of A3 C3 3abc Mathematics Topperlearning Com 3vrgnejoo



The Value Of Determinant A B B C A B C C A B C A A B C Is Studyrankersonline




Prove A 3 B 3 C 3 3abc 1 2 A B C A B 2 B C 2 C A 2




Find The Value Of A 3 B 3 C 3 3abc If 1 A B C 8 Ab Ca 19 2 A B C 5 A 2 B 2 C 2 1 Youtube




If A B C 5 And Ab Ca 10 Prove A 3 B 3 C 3 3abc 25 Cbse Class 9 Maths Learn Cbse Forum



A B C 2 Formula



If A B C 0 Then Find The Value Of B2 Ca C2 Ab Polynomials Maths Class 9




If A B 3 And Ab 2 Then Find A 3 B 3




A 3 B 3 C 3 3abc Formula A B 2 A 2 B 2 2ab Proof Derivation Of Algebraic Identities Youtube Youtube




Find The Value Of A 3 B 3 C 3 3abc If 1 A B C 8 Ab Ca 19



What Is The Value Of A B C 3 Quora



If A B C 5 And Ab Ca 10 Then Prove That A3 C3 3abc 25 Studyrankersonline



If The Mid Points Of The Sides Ab Ca Of A Triangle Are 1 5 1 0 4 2 2 3 4 Respectively Then The Length Of The Median From C To Ab Is What Quora




What Are Various Forms To Write A B C A Whole Cube Quora




Prove That A3 C3 3abc A B C B2 C2 Ab Ac By Taking Lhs Brainly In




A B C 2 3 Ab Ca Youtube
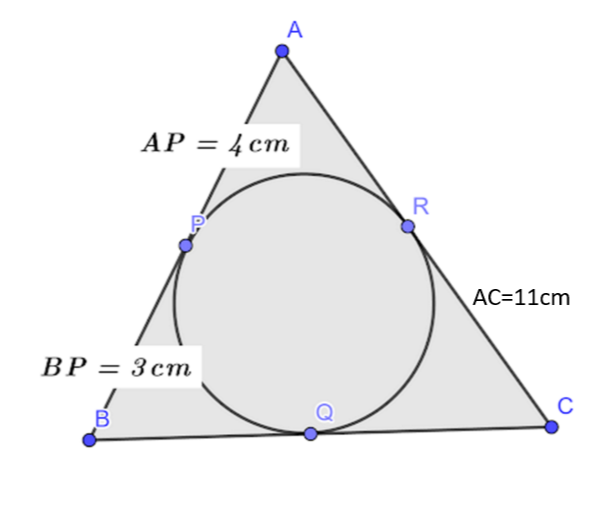



In The Figure The Sides Ab And Ca Of A Triangle Class 10 Maths Cbse




Prove That 1 A A 3 1 B B 3 1 C C 3 A B B C C A A B C




Misc 4 Show That Either A B C 0 Or A B C Miscellaneous




Ab Ca Does Not Exceed Cc




Factorise A B Whole Cube B C Whole Cube C A Whole Brainly In



0 件のコメント:
コメントを投稿