底が楕円として、楕円錐の体積を算出したかった。 keisanより 長径a,短径bの楕円の面積S=πab、半径rの円の面積はS=πr 2 ですので、直円錐の体積の半径rに開平√ (a*b)を計算して代入すれば、楕円錐の体積が求まります。 5 2338 男 / 歳未満 / 学生 / 役に立った / 使用目的 これからの数学との戦い ご意見・ご感想 円錐の側面積は 母線×底面の半径×πで出て先に整理した面積の求め方を参照させる。 (例)底面積s6×4 =24 高さh7 自分でノートに見取図をかいて,辺,半径,高さ などに長さを記入する。 見取図の書き方ができるかどうか確認する。 ま と め 今日の学習のまと めをする。 錐体の体積=T:a=底面の面積 b=上面の面積 c=aとbの真中の面積 h=高さ とすると、 Sor という公式がある。この公式は、台の体積はおろか、三角形の面積まで求めることができる。 例えば、台形、半球を求めてみよう。 半球の体積=(πr 2 +3/4πr 2 3

円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者
円錐 高さ 求め方 公式
円錐 高さ 求め方 公式-V = 1 3Sh = 1 3πr2h V = 1 3 S h = 1 3 π r 2 h ここで、V は円錐の体積、S は底面積、h は高さを表します。 また、2行目における π は円周率、r は底面の円の半径です。 円錐の体積を求めるには、この公式に底面の半径 r と高さ h を代入すればよいだけです。 このページの続きでは、例題を使って、この公式の使い方を説明しています。 もくじ 円錐の体積を求める公式円錐の表面積を求める公式 は、次の通りです。 S = πr(r R) = π ×(底面の半径)× {(底面の半径) (母線の長さ)} S = π r ( r R) = π × (底面の半径) × { (底面の半径) (母線の長さ) } 底面の半径 r、母線の長さ R の円錐 1行目の文字について、S は円錐の表面積、r は底面の円の半径、R は母線の長さを表します。 手っ取り早く円錐の体積を求めるには、この




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室
円錐の表面積 体積計算の簡単な求め方を解説 公式を証明しよう 中学数学で習う円錐の表面積体積の求め方 円柱とはどう違うんだっけ 表面積って何か公式あったよね なんて忘れかけていませんか 高校数学大学受験でも頻出の円錐 今一度円錐の求め方公式の覚え方を再確認しましょう 扇の中心角の求め方を知らない人は、 扇形の中心角の求め方3パターンを見てみてね ちなみに、中心角を求める公式もあって $中心角 = 360 \times \dfrac{半径}{母線}$ こんなのもあるから、今日テストの人はさっと覚えてもいいかもしれないね けど!円錐の体積と公式の問題、高さの求め方 下図の円錐の体積を、公式を用いて求めましょう。 上記の値を公式に当てはめれば良いので簡単ですね。 また下図の円錐の体積=15m 3 、半径=2mのとき、高さを求めてください。 円錐の高さは下式を用いて算定します。
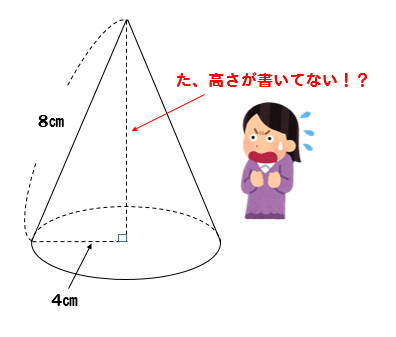
(円錐の高さ) = √(斜辺の二乗) (その他の1辺の二乗) = √ (12)² – 3² = √135 になるね。 おめでとう^_^ 円錐の高さもゲットだね! まとめ:円錐の高さの求め方は三平方の定理でとどめ! 円錐の高さを求めるのはむずそう。台形の1辺・面積(3辺の長さと高さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 ひし形の面積 平行四辺形の面積 (底辺と高さから) 平行四辺形の面積(底辺と高さから) 平行四辺形の面積 (2辺と夾角から) q 底面の半径が3㎝、高さが6㎝の円錐aがあり、この 円錐aと体積が等しい円柱bがある。 円柱bの底面の半径が 3㎝のとき、円柱bの表面積を求めなさい。 (問題文の下に円錐aの図が書いて
円柱の体積、表面積の求め方はこれでバッチリ! 円錐の表面積、中心角の求め方を解説!裏ワザ公式も!←今回の記事 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう!円錐の表面積の求め方 問題を学ぶにあたって 体積を求める場合と同じく、円錐の表面積を求める場合にも公式が存在します。 ということは、この公式させ覚えてしまえば、円錐の表面積が問われる問題は簡単に処理できるように思わ四角錐の表面積の求め方公式 小学生・中学生の勉強 計算公式正四角錐の体積の求め方がわかる3ステップ 四角錐台の公式(体積・側面積・表面積) 数学 エクセルマニア;




三平方の定理を利用して四角すい 円すいの体積を求める 無料で使える中学学習プリント




三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ
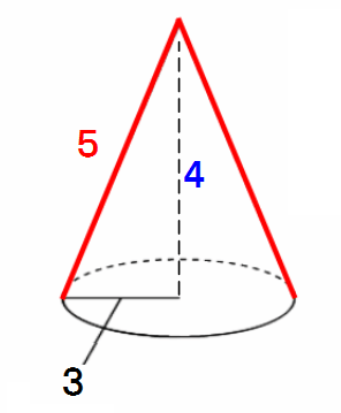
先に、公式が知りたい人のために公式をサクッと紹介 公式は $S=\pi r(lr)$ だよ! 記号の意味が分からない人は図も見てね 円錐の表面積は、上の公式を覚えておけば楽勝だよ♪ それでは、例題を使って円錐の表面積の求め方を確認してみましょう。 次の円錐の表面積を求めなさい。 まずは公式にしたがって円錐の底面積を求めましょう。 底面積 次は母線と半径をかけて問題図の円錐の体積を求めなさい。 ○錐の体積 → 底 面 積 高 さ 底 面 積 × 高 さ × 1 3 V = 1 3 S h 円錐の底面は円なので、底面積は 3 × 3 × π = 9 π 高さは 4 c m




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
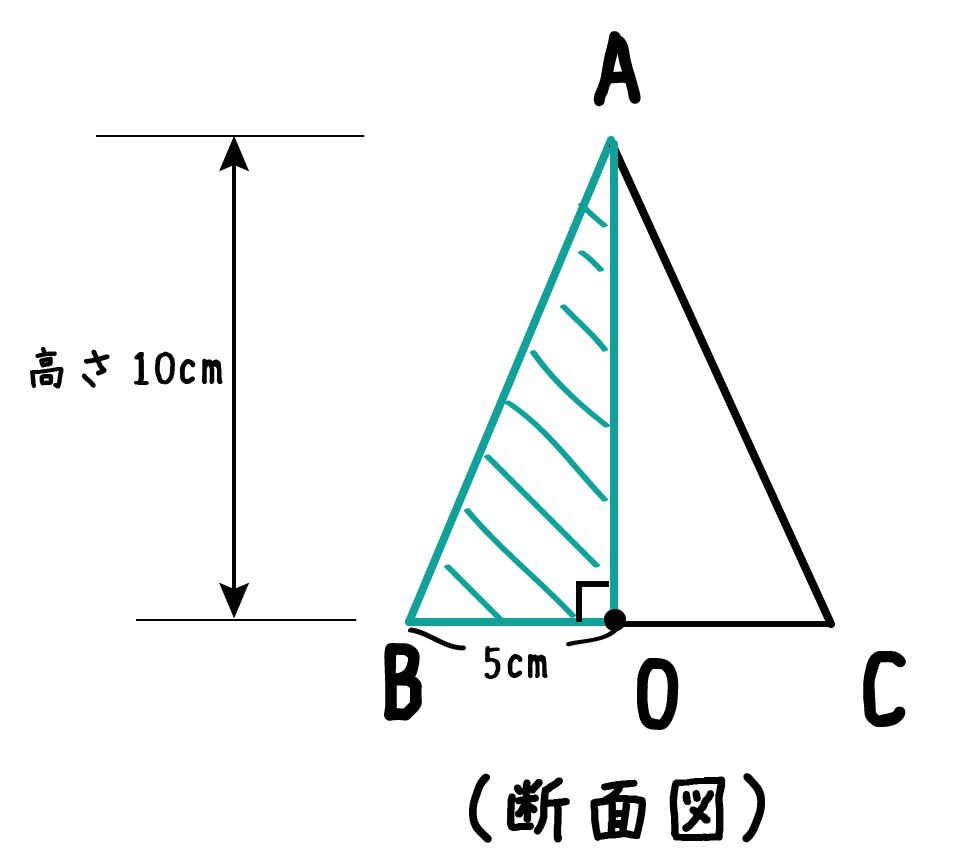
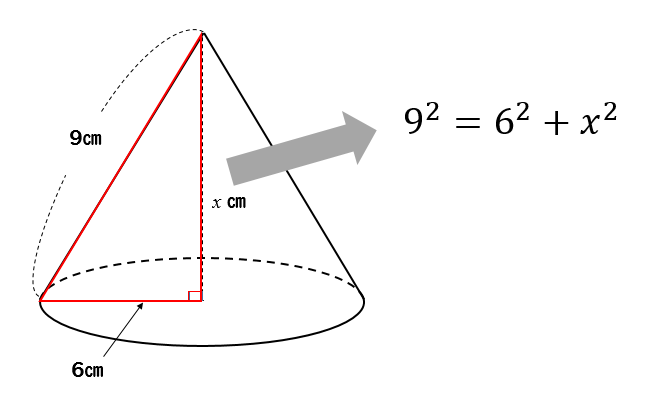
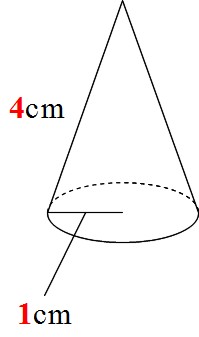
どらえもんの算数は、底面積と高さが同じ角柱と角錐を 作って、水を使って、角錐3杯分の水が角柱に入ることの実験になっていた。 頭ごなしに公式を覚えさせるのに比較すれば随分まともだが、 これでは、正確に3なのかどうか分らない。答えを求めておくと 高さは $$6^2=2^2x^2$$ $$x=4\sqrt{2}$$ 体積は $$4\pi \times 4\sqrt{2} \times \frac{1}{3}$$ $$=\frac{16}{3}\sqrt{2}\pi cm^3$$ となります。 これで 展開図で出されても大丈夫ですね! 半径がわからないパターン ここまでずっと 円錐の高さのことばかり言ってきましたが三角柱の体積の求め方の公式って?? こんにちは!この記事をかいているKenだよ。登山で日焼けしたね。 三角柱の体積の求め方には公式があるんだ。 三角形の底辺の長さをa、底辺からの高さをb、立体の高さがhっていう三角柱を想像してみて。




中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




円錐の体積ってなんであの公式なの Webty Staff Blog
角柱・角錐・円柱・円錐の体積の求め方がわかりません。公式を教えてください。 進研ゼミからの回答 立体の体積はこれから先も利用するので,それぞれしっかり覚えておきましょう。 ※ このQ&Aでは円錐のときも同じように展開図を書いて考えます。 ですが、円錐の場合には展開図を書くにあたって 側面であるおうぎ形の中心角を求める必要があります。 中心角の求め方は、こちらの裏ワザ公式を利用すると簡単ですね(^^) 円錐の高さの求め方 理論と式 中等教育と学校 2月 中1 数学 空間図形11 円錐 12分 Youtube 成城中 算数の図形問題 プロが教える重要ポイント ラベル 円錐 高さ 求め方, 円錐 高さ 求め方 公式 0 件のコメント




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




体積の求め方 計算公式一覧
関連記事はこちら 中学数学円錐の表面積の求め方と公式図たくさん 中学数学円錐の高さの求め方頻出パターン 中学数学円錐の中心角の求め方3パターン 円錐の側面積の求め方ですね。 円錐の側面積の求め方 母線×底面の半径×314 確かにこの公式を覚えておけば側面積を即答できるため、圧倒的に有利なのですが、それは覚えていられる間の話。 もし 忘れたり混乱したりすると、求められなくなって 円錐の関連記事はこちら 中学数学円錐の体積の求め方・公式サクッと 中学数学円錐の高さの求め方頻出パターン 中学数学円錐の中心角の求め方3パターン




計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




高さの分からない円すい展開図 どうやって立体の体積を求めるの
円錐の表面積の求め方は完全パターン化できる! 表面積の求め方 計算公式一覧 Scipursuit 円錐(すい)の表面積や四角錐,五角錐の体積の求め方; めっちゃ簡単! ? 円錐の体積の求め方を解説 投稿日:年6月25日 こんにちはこんばんは! taraといいます。 6月も終わりを迎えようとしている今日この頃ですが、 空模様はまだまだ梅雨真っただ中ですね。 僕自身ジメジメした気候は嫌いなんで、 これを体積の公式に当てはめて、 $\dfrac{16}{3}\sqrt{2}\pi = \dfrac{4}{3} \pi h $ ∴ $4\sqrt{2}= h $ だね! まとめ 円錐の高さを求める問題は、ほぼこの2パターン!




円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com




中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
円すいの展開図、中心角の公式を知って5秒で解こう♪ 面積 面積 円すいの展開図の中心角を求めなさい。 円周率は314とします。 知りたがり 何に注目 すれば体積の公式、円形の面積の求め方は下記が参考になります。 体積の公式は?1分でわかる求め方と覚え方、一覧、三角柱、円柱、三角錐の体積 円の断面積は?1分でわかる意味、公式、計算方法と求め方、直径との関係 100円から読める!ネット不要!問題2 (円錐の展開図) 右の図のように,底面の半径が3cm,高さが4cm,母線の長さが5cmの円 すい 錐がある。 次の(1),(2)に答えなさい。 (1) この円錐の体積を求めなさい。




角錐 円錐の体積と表面積の公式 数学fun




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
円すいの体積の公式 底円の半径を r 、高さを h とすると 上図の円錐の体積は 体 積 底 面 積 高 さ 体積 V = 底面積 × 高さ × 1 3 = r × r × 314 × h × 1 3よってVは、x=、つまり底辺の半径がcm、高さが10cmのときに最大となります。 その値は、 です。 ・ 最大最小値を使って箱の体積を求める ・最大最小値を使って円錐の体積を求める ・ 3次関数の最大値と最小値の求め方 (極大値と極小値の違いのような問題、円錐台を2分割にする高さを求める計算式です。 人参を円錐(R1=0)とすると、太いほうから1:4に分ける位置で切ればいいことになります。 上部の半径R1 下部の半径R2




中学数学 円錐の体積の求め方 公式 サクッと なぜか分かる はかせちゃんの怪しい研究室




公式を図解 すい体の体積 円すいの表面積の求め方




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




直円錐の体積 高精度計算サイト




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




高さの分からない円すい展開図 どうやって立体の体積を求めるの




高さの分からない円すい展開図 どうやって立体の体積を求めるの




円錐 体積 求め 方 公式を図解 すい体の体積 円すいの表面積の求め方 Amp Petmd Com




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室



中学数学 円錐の 母線の長さ がわかる2つの求め方 Qikeru 学びを楽しくわかりやすく




公式を図解 すい体の体積 円すいの表面積の求め方



重心を求める問題で円錐の体積 底面積 高さ 3円錐の重心の位置 高さ 4を Yahoo 知恵袋



3




円錐の表面積の求め方 公式と計算例




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学



三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




円錐の体積を求める Youtube




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円柱の表面積と体積を求める公式 具体例で学ぶ数学




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学



三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ




公式を図解 すい体の体積 円すいの表面積の求め方




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室




中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




円錐の体積の求め方 公式 小学生 中学生の勉強




中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室




簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



1
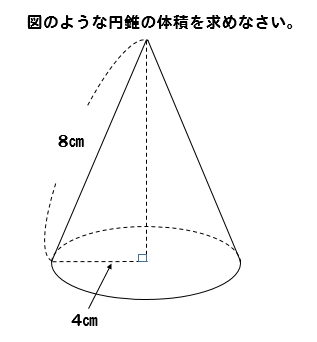



三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




円錐の体積ってなんであの公式なの Webty Staff Blog




高校数学 球に内接する直円錐の体積 側面積の最大値 受験の月




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
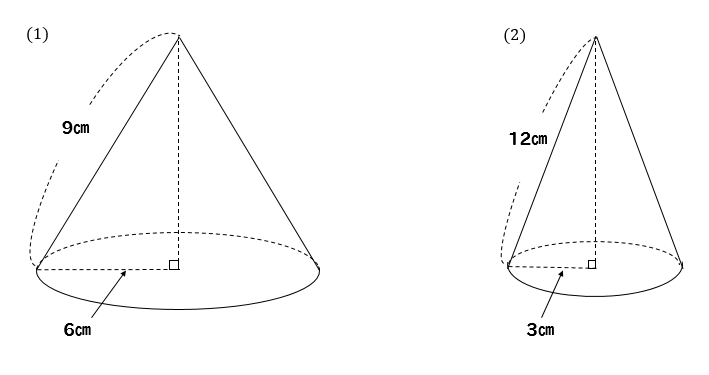



三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ




底面の半径が5で高さが12の直円すいの体積で 1 体積を求める Clear




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室




中学数学 円錐の中心角の求め方 3パターン なぜか分かる はかせちゃんの怪しい研究室




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



緊急です この円錐の下の円の半径と円錐台の高さの求め方を教えて下さい Yahoo 知恵袋




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学



3
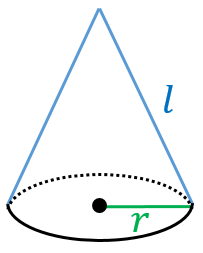



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学
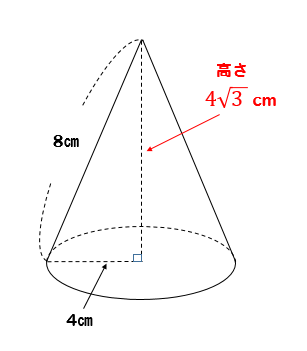



三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ



1
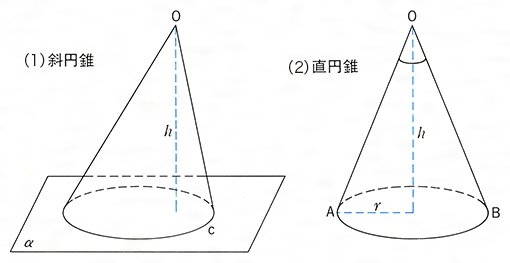



円錐とは コトバンク
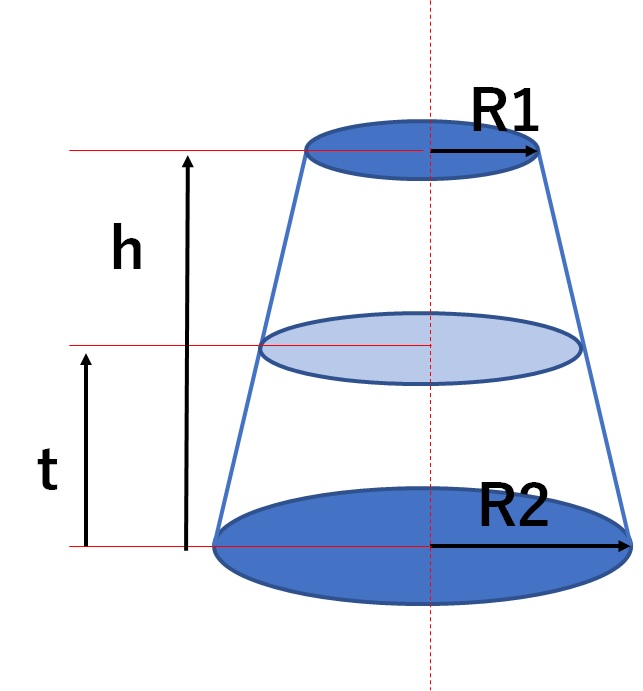



円錐台の体積を半分にする高さを計算 高精度計算サイト




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




角錐 円錐の体積と表面積の公式 数学fun




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




三平方の定理を利用して四角すい 円すいの体積を求める 無料で使える中学学習プリント




高さの分からない円すい展開図 どうやって立体の体積を求めるの




角錐 円錐の体積と表面積の公式 数学fun
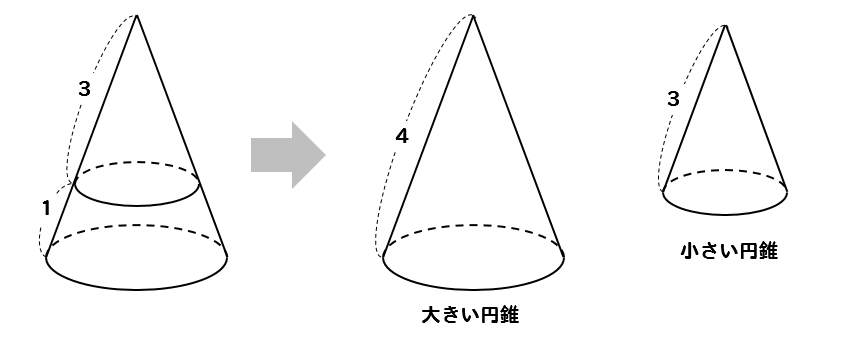



中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ



円錐 体積 求め 方 公式を図解 すい体の体積 円すいの表面積の求め方 Amp Petmd Com
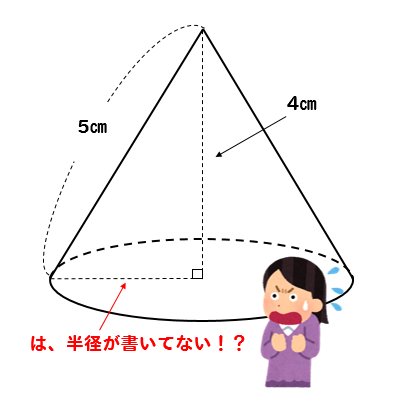



三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ




表面積の求め方 計算公式一覧
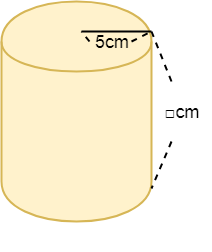



円柱の体積の求め方 公式 小学生 中学生の勉強
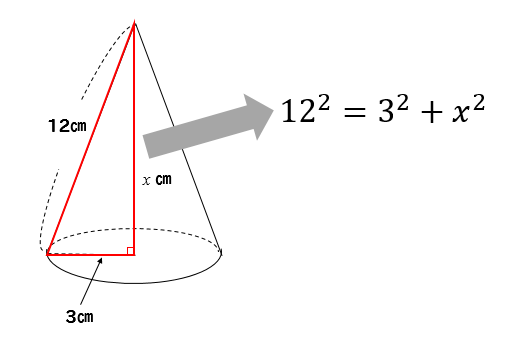



三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ



積分計算による体積の求め方 断面積の積分や回転体の体積 受験辞典




円柱の体積の公式 円の面積の求め方を覚えていないとダメ 中学や高校の数学の計算問題



円すいの高さの求め方を教えて下さい できたらr でお願いします ど Yahoo 知恵袋




中3 三角形の相似 円錐の体積比 日本語版 Youtube




Hd限定円錐 体積 の 求め 方 ページを着色するだけ
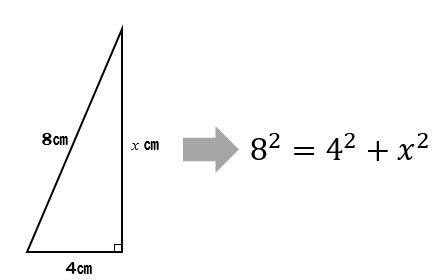



三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ
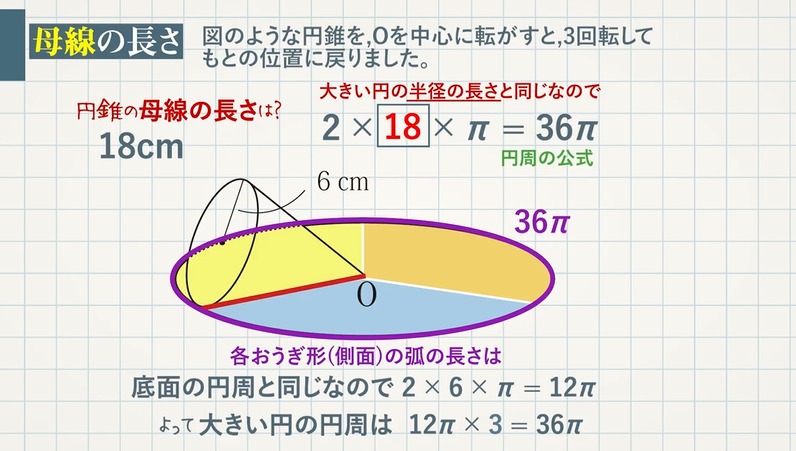



円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




体積の求め方 計算公式一覧




中3数学 円錐の高さと体積 5分で学習 Youtube



円錐の体積と公式は 1分でわかる公式 問題と高さの求め方 証明



三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者



Math 円錐の側面積が1秒で求められる公式 中学生 働きアリ




円錐の表面積 側面積 体積の求め方教えてください Clear




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師




円すい 円錐 の体積の求め方と問題 小学数学 Irohabook




3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




円錐の表面積の求め方 You Look Too Cool




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学



0 件のコメント:
コメントを投稿